Čtvrtá série třicátého šestého ročníku KSP
Celý leták v PDF.
Řešení úloh
- 36-4-1: Oprava vzducholodi
- 36-4-2: Megasněhulák
- 36-4-3: Sklad s bednami
- 36-4-4: Heslo
- 36-4-S: Nechme stromy růst
- 36-4-X1: Počet koček
 36-4-1 Oprava vzducholodi (Zadání)
36-4-1 Oprava vzducholodi (Zadání)
Nejprve si označme počet hran v grafu jako M, protože na něm bude záviset naše složitost (cílíme na lineární algoritmus v délce vstupu). Ze zadání máme počet vrcholů označený N.
Určitě úkoly, které doděláme jako poslední, jsou kritické, protože jejich prodloužení přímo vede k celkovému prodloužení. Dále musíme uvážit závislosti posledních úkolů, protože když se poslední z těchto závislostí prodlouží, znamená to, že také odloží práci. Podobně také poslední závislosti posledních závislostí posledních úkolů a tak dále. Z toho už můžeme vypozorovat hledaný algoritmus.
Nejprve si graf závislostí topologicky seřadíme. Pak si u každého úkolu spočítáme, kdy začne a kdy skončí. Vrcholy bez závislostí začnou v čase 0 a skončí v čase jejich doby trvání. Zbytek vrcholů budeme postupně procházet a díky topologickému seřazení vždy narazíme na vrchol v momentě, kdy už máme všechny jeho závislosti zpracované a tedy víme, že začne v čase maxima z časů konců jeho závislostí.
V další fázi už využijeme naši myšlenku z prvního odstavce. Množinu úkolů, které skončí jako poslední označíme U0 (může jich být víc, pokud skončí ve stejnou dobu). Ty přidáme do seznamu úkolů, které Kevina zajímají, protože kdyby se protáhly, tak to prodlouží celý projekt.
Dále opakujeme pro rostoucí i následující kroky:
- Pokud je Ui prázdná množina, už nejsou žádné úlohy, u nichž by malé zdržení způsobilo celkové zdržení, takže můžeme skončit.
- Jinak se pro každou úlohu u z Ui podíváme na její předchůdce a z nich vybereme ty, jejichž čas konce se rovná času začátku u (to jsou ty, u kterých by se prodloužení přeneslo na prodloužení u). Z nich ještě vyřadíme ty, které již jsou na Kevinově seznamu. Zbylé úlohy označíme Ui+1 a opět je přidáme na Kevinův seznam.
Tímto nalezneme všechny úlohy, které by stavbu Kevinovy vzducholodi protáhly, ale ještě nám zbývá vyřešit složitost algoritmu. Topologické seřazení trvá O(N+M), počítání časů začátku a konců je lineární (postupně procházíme všechny vrcholy). A nakonec cyklus, ve kterém hledáme úlohy do Kevinova seznamu, je také prohledávání grafu, které trvá O(N+M), takže celková složitost je O(N+M).
 36-4-2 Megasněhulák (Zadání)
36-4-2 Megasněhulák (Zadání)
Můžeme si všimnout, že na pořadí koulí na vstupu vůbec nezáleží. Podobně je nám při stavbě sněhuláků jedno, jak přesně velké koule jsou, zajímá nás jen, které jsou stejně velké. Dokonce nás ani nezajímá, které koule jsou menší a které větší: pokud nám někdo přidělí K koulí různých velikostí v libovolném pořadí, tak si z nich můžeme postavit sněhuláka jen jedním možným způsobem. Důležité je jen to, abychom každou skupinu koulí počítali jen jednou, nezávisle na pořadí.
Pro každou velikost koule si tedy spočítáme, kolik koulí této velikosti máme k dispozici. K tomu můžeme použít například hešovací tabulku. Počet různých velikostí koulí označíme M. Počet koulí první z dostupných velikostí označíme V1, počet koulí druhé V2, a tak dále.

Úlohu můžeme vyřešit pomocí dynamického programování. Pokud nevíte, v čem dynamické programování spočívá, můžete si přečíst naší kuchařku o něm. Ve zkratce se jedná o metodu řešení problémů, při které se postupně řeší větší a větší podproblémy zadaného problému, každý z nich jako kombinace řešení menších podproblémů.
Zadefinujeme dpi, j jako počet možných sněhuláků z j koulí, které můžeme postavit, pokud použijeme jen koule prvních i velikostí. Řešením úlohy bude dpM, K: Počet sněhuláků z K koulí, které mohou používat koule všech dostupných velikostí.
Začneme s jednoduchými případy: Každé dpi, 0 bude určitě 1, protože sněhuláka z nula koulí můžeme postavit jen jedním způsobem, a to tak, že žádné koule nepoužijeme. Podobně pro j ≤ 1 bude dp0, j rovno 0, protože neprázdného sněhuláka nemůžeme nijak postavit, pokud nemáme k dispozici žádné koule.
Jak spočítáme dpi, j pro větší i nebo j? Sněhuláky, které smí používat jen koule prvních i velikostí, můžeme rozdělit na dvě skupiny: ty, které kouli i-té velikosti používají, a ty co ne. Sněhuláka, který takovou kouli obsahuje, můžeme postavit tak, že vezmeme jednoho z dpi - 1, j - 1 o kouli menších sněhuláků, co nepoužívají velikost i, a přidáme do něj jednu z Vi koulí správné velikosti. Počet takovýchto sněhuláků bude Vi dpi - 1, j - 1. Počet sněhuláků, které i-tou velikost nepoužívají, bude jednoduše dpi - 1, j. Počet sněhuláků obou druhů jednoduše sečteme, čímž získáme šikovný vzoreček:
Všimneme si, že abychom mohli spočítat dpi, j, tak stačí, abychom měli spočítané všechna dpi′, j′ pro i′< i a j′< j. Pokud si hodnoty dp představíme jako tabulku o m+1 sloupcích a k+1 řádcích, pak můžeme její hodnoty počítat postupně zleva doprava a seshora dolů, aniž bychom kdykoliv potřebovali znát hodnotu políčka, které jsme ještě nespočítali. Takto spočítáme dpM, K v čase O(MK) ⊆ O(NK).
Při řešení úlohy narazíme na to, že počet možných sněhuláků má tisíce číslic. V některých programovacích jazycích se takto velké číslo vůbec nevejde do běžných číselných proměnných, jiné jazyky (např. Python) sice libovolně velká čísla podporují, ale matematické operace s nimi trvají dlouho. Zadání po nás ale naštěstí nechce celý výsledek, ale jen jeho zbytek po dělení číslem 1 000 000 007. Tento zbytek po dělení nemusíme počítat až na konci, ale můžeme jej počítat průběžně po každé aritmetické operaci, aniž bychom tím ovlivnili výsledek. Tím zajistíme, že čísla, se kterými pracujeme, jsou rozumně malá. Více o tomto pozoruhodném pravidle se můžete dočíst v naší kuchařce o teorii čísel.
 36-4-3 Sklad s bednami (Zadání)
36-4-3 Sklad s bednami (Zadání)
Vyřešme nejprve otázku značení. Počet beden budeme v tomto textu značit B a délku posloupnosti pohybů N.
Pomalé řešení
Úlohu můžeme řešit pomocí simulace jednotlivých pohybů vozíku ve skladišti. Založíme si binární vyhledávací strom, který bude v průběhu algoritmu udržovat aktuálně nějakou bednou zabrané pozice a následně začneme posouvat vozík přesně podle jednotlivých instrukcí.
Všimněme si, že když vozík narazí během simulace do souvislé řady beden, tak její hromadné posunutí o 1 ve směru pohybu odpovídá přesunutí bedny, do které narazil, na první volné pole ve směru pohybu. To je zaručeno nerozlišitelností beden.
Jakmile tedy po přesunu vozíku zjistíme, že se nachází na poli zabraném nějakou bednou, začneme procházet pole ve směru pohybu a kontrolovat jejich obsazenost pomocí vyhledávacího stromu, dokud nenarazíme na první volnou pozici. Následně z vyhledávacího stromu odstraníme původní pozici a vložíme do něj pozici novou.
Na konci simulace projdeme náš binární vyhledávací strom vypíšeme všechny pozice, jež obsahuje.
Časová složitost tohoto algoritmu bude rovna O(NB log B), neboť v každém z N kroků simulace potřebujeme provést až B operací s binárním vyhledávacím stromem.
Rychlejší řešení
Zůstaneme u simulace, nicméně ji znatelně urychlíme.
Nahlédneme, že nás v každém kroku simulace nejvíce zpomaluje přesun beden, konkrétně hledání první volné pozice ve směru pohybu.
Tu lze však najít mnohem rychleji, než průchodem až B beden. Vybudujeme si za tímto účelem binární vyhledávací strom zvlášť pro každý řádek a sloupec. Nebudeme v nich nicméně tentokrát ukládat jednotlivé pozice beden, ale celé souvislé úseky zabrané bednami.
Vyhledávací strom nemusíme pro uchování úseků nijak přizpůsobit, využijeme toho, že se úseky na daném řádku či sloupci nikdy nepřekrývají, takže je můžeme ve stromu porovnávat třeba podle jejich levých souřadnic.
Nyní k průběhu samotné simulace. Předpokládejme, že se vozík pohnul směrem doprava či doleva. Pokud se pohnul nahoru nebo dolů, budeme postupovat podobně, jen zaměníme řádky a sloupce.
Nejprve zkontrolujeme, zda se vozík přesunul na pozici zabranou bednou, tedy zda leží v okraji nějakého úseku. Pokud se vozík pohnul doprava, vyhledáme ve stromu odpovídajícímu aktuálnímu řádku přímo souřadnici x vozíku. V případě, že se vozík pohnul směrem doleva, nalezneme ve stromu nejbližší úsek zleva a porovnáme s vozíkem pravou souřadnici úseku.
Zjistíme-li, že se vozík nachází na poli zabraném bednou, vyjmeme nalezený úsek ze stromu pro aktuální řádek a zvětšíme či zmenšíme jeho krajní souřadnice podle směru pohybu. Nemůžeme jej však nyní jen tak vrátit zpět do stromu, posunutím úseku mohlo totiž dojít k jeho spojení se sousedním.
Nalezneme tedy ve stromu nejbližší sousední úsek, a pokud mezi ním a posunutým úsekem neleží žádné pole, spojíme je a výsledek vložíme zpět do stromu.
Aktualizovali jsme údaje pro daný řádek, nicméně je třeba upravit data i ve stromech, jež odpovídají sloupcům.
Vzpomeneme si, že posunutí úseku o jedna libovolným směrem odpovídá přesunutí bedny, do které vozík narazil, na první volné místo ve směru pohybu.
Stejným způsobem provedeme i aktualizace sloupců, vyjmeme bednu ze stromu odpovídajícímu sloupci, kde se nacházela bedna, do které vozík narazil, a vložíme ji do stromu odpovídajícímu sloupci, kde se původně nacházela první volná mezera. Nesmíme zapomenout, že pracujeme s intervaly a ne se samostatnými bednami. Operace vyjmutí odpovídá odstranění souvislého úseku, jehož je bedna součástí, a jeho následnému nahrazení až dvěma úseky vzniklými odstraněním dané bedny. Operace vložení bedny zase odpovídá vložení úseku délky 1, nicméně může být nutné tento interval spojit se sousedními úseky.
Stavba stromů
Před začátkem simulace je nutné nejprve rychle postavit binární vyhledávací stromy pro dané řádky a sloupce.
K tomu potřebujeme nezbytně vědět, jaké bedny jsou na stejném řádku či sloupci. Dále se nám bude hodit znalost vzájemného pořadí beden na jednotlivých řádcích a sloupcích, neboť se dá binární vyhledávací strom postavit s pomocí setřízené posloupnosti prvků v lineárním čase.
Obě informace můžeme snadno zjistit pomocí dvou lexikografických uspořádání beden, jednoho řazeného primárně podle x a druhého řazeného primárně podle y.
Ta bychom mohli nalézt v O(B log B) pomocí libovolného třídicího algoritmu založeného na porovnávání, nicméně se s něčím takovým nespokojíme.
Nejprve nahlédneme, že nepotřebujeme nutně stromy pro všechny řádky a sloupce. Pokud budeme například třídit primárně podle y a sekundárně podle x, tak nám stačí vybudovat jen stromy odpovídající řádkům vzdáleným nejvýše N od řádku, na kterém leží vozík ve výchozí pozici. To platí, protože potřebujeme stromy jen kvůli simulaci horizontálních pohybů vozíku a aby bylo možné na těchto řádcích přesouvat bedny doleva či doprava, je nutné se na tyto řádky nejprve dostat. To ovšem není pro žádný řádek vzdálenější než N z důvodu omezené délky posloupnosti pohybů možné.
Totéž uvážíme i pro sloupce a vyloučíme jakýkoliv sloupec vzdálenější od výchozí pozice více než N.
Odkazy na jednotlivé stromy si tedy můžeme uložit do dvou polí velikosti O(N), což znamená, že jsme schopni přistoupit k libovolnému stromu v konstantním čase.
Platí, že se dokonce ani na zbývajících řádcích a sloupcích nemusíme zabývat vždy nutně všemi bednami. Některé bedny totiž mohou být příliš vzdáleny na to, aby dokázal vozík v N pohybech nějak ovlivnit jejich pozici. Leží-li bedna a vozík na stejném řádku či sloupci a nachází se mezi nimi alespoň N+B polí, nemůže vozík s N pohyby tuto bednu nikdy přesunout.
Zkusme se zamyslet, proč tohle platí. Vozík může bednu přesunout buď přímo, to dojde ke kontaktu vozíku s bednou, a nebo nepřímo, kdy je bedna tlačena jinou bednou.
K přímému přesunutí takto vzdálené bedny určitě dojít nemůže, protože má vozík k dispozici jen N pohybů.
U nepřímého přesunutí už to není tak jednoznačné. Aby mohl vozík nějak ovlivnit pozici bedny, musí mezi vozíkem a bednou ležet souvislý úsek beden. Na počátku se nicméně mezi bednou a vozíkem nachází minimálně N prázdných polí. Na každé přiblížení vozíku směrem k bedně potom můžeme nahlížet jako na odstranění jednoho prázdného pole z oblasti mezi cílovou bednou a vozíkem. I kdyby tedy po N posunech vozíku směrem k bedně byly odstraněny všechna prázdná pole, tak by již neměl vozík k dispozici žádný pohyb k přesunutí bedny. Můžeme si též rozmyslet, že nám nijak nepomůže přecházet mezi řádky či sloupci.
Z tohoto pozorování plyne, že v našich stromech vybudovaných pro řádky či sloupce nepotřebujeme žádné bedny ve vzdálenosti větší než N+B od výchozího x či y. To znamená, že souřadnice všech beden, které potřebujeme setřídit, jsou čísla v rozsahu o velkosti O(N+B). Můžeme tedy obě lexikografická uspořádání nalézt pomocí přihrádkového třídění v O(N+B) a v takovém čase jsme i schopni postavit samotné stromy.
Vypsání pozic všech beden
Protože již ve vyhledávacích stromech neuchováváme nutně všechny bedny, není vypsání zabraných pozic tak přímočaré.
Pozice všech beden, které se nenachází v žádném vyhledávacím stromu, se nemohly během simulace změnit, takže je můžeme rovnou vypsat.
Zbylé bedny se již nachází zakódovány v úsecích v jednotlivých stromech. Můžeme tedy všechny stromy v O(B) projít a z úseků následně vygenerovat souřadnice beden.
Jen si ještě musíme dát pozor, že jsou některé pozice zakódovány ve stromech dvakrát, jednou ve stromu pro odpovídající řádek a podruhé ve stromu pro odpovídající sloupec.
Každá taková bedna má rozdíl obou souřadnic s výchozí pozicí menší nebo roven N, takže jsme schopni snadno v každém stromu rozhodnout, jaká jeho část je obsažena ve více vyhledávacích stromech a zamezit duplicitním informacím na výstupu.
Časová a paměťová složitost
Nejprve jsme v O(N+B) postavili jednotlivé stromy. Následně jsme v každém z N kroků simulace provedli konstantní počet operací s binárním vyhledávacím stromem velikosti O(B) a na závěr jsme v O(B) nalezli a vypsali všechny bednami zabrané pozice. Časová složitost tohoto algoritmu tak bude O(N log B + B).
Paměťová složitost algoritmu bude O(N+B), neboť k přihrádkovému třídění potřebujeme O(N+B) paměti a i zabraný prostor všemi stromy spolu s pomocnými poli s odkazy nepřesáhne O(N+B).
Ještě větší zrychlení
Můžete si jako cvičení rozmyslet, že se dá algoritmus drobnou úpravou urychlit na O(N log min(B, N) + B). Stačí k tomu nalézt na každém řádku přesnější odhad pro nejbližší bednu, kterou nemůže vozík na daném řádku či sloupci nikdy přesunout.
Dále si všimněme, že jsme sice při stavbě stromů využívali toho, že pracujeme s malým rozsahem souřadnic, nicméně jsme tuto skutečnost vůbec nevyužili při samotné simulaci.
Pro rychlou práci s celými čísly v pevně daném rozsahu existuje zvláštní datová struktura zvaná y-fast strom (v angličtině y-fast trie). Časové složitosti jednotlivých operací v tomto stromu již nezávisí na počtu v něm uložených hodnot, ale na jejich rozsahu. Zároveň však strom nadále zabírá lineární množství paměti vzhledem k počtu obsažených prvků. Za nízké nároky na paměť bohužel platíme nutností použít hashování a tedy i horší časovou složitostí některých operací v nejhorším případě. Dá se však ukázat, že tyto operace poběží dostatečně rychle alespoň průměrně amortizovaně.
Nechť je U rozsah celých čísel, se kterými pracujeme, a N počet prvků stromu.
Operace nalezení konkrétního čísla i nejbližší nižší a vyšší hodnoty bude vždy trvat O(log log U). Operace vkládání a mazání prvků již nemusí být pokaždé tak rychlé, nicméně budou trvat O(log log U) průměrně amortizovaně. Se znalostí vzájemného pořadí prvků jsme schopni postavit samotný strom v průměru v O(N).
To jsou všechny operace, které od našeho stromu potřebujeme. Protože je rozsah souřadnic velký O(N+B), bude mít algoritmus po použití této datové struktury průměrnou časovou složitost O(N log log(N+B) + B).
Paměťová složitost tohoto algoritmu zůstane O(N+B).
 36-4-4 Heslo (Zadání)
36-4-4 Heslo (Zadání)
Vzhledem k tomu, že zadání není moc obsáhlé, nezbývá nám nic jiného než zkusit nějaké heslo vytvořit a odevzdat ho. Tam zjistíme hlavní princip úlohy – odevzdávátko má seznam 10 pravidel, které heslo musí splňovat. Ty kontroluje v daném pořadí, kde za splněné pravidlo dá bod a nesplněné vypíše a nekontroluje další pravidla.

Zde je seznam pravidel pro nahlédnutí. V hranatých závorkách značíme údaje, které se měnily pro konkrétní vygenerovaný vstup:
- Heslo musí obsahovat malé písmeno, velké písmeno a číslo.
- Počet malých a velkých písmen se může lišit nejvýše o 1.
- Součet římských číslic musí být roven aktuální minutě.
- Součet atomových čísel prvků v hesle musí být [číslo].
- Heslo musí obsahovat jméno města na [souřadnicích].
- Heslo musí obsahovat jednoho z našich sponzorů.
- Heslo nesmí obsahovat [písmeno].
- Heslo musí obsahovat kód úlohy s [hrošíkem] v zadání.
- Heslo musí mít prvočíselnou délku.
- Pro potvrzení zadej heslo znovu:
Nicméně se brzo ukáže, že pravidla se navzájem ovlivňují – Např.
změna minuty mění počet I v hesle, a přidání těch mění
součet atomových čísel. A tak podobně.
Navíc římské minuty a platnost vstupů nám nedávají moc času, což úlohu činní ručně neřešitelnou. Ale tak si pojďme napsat program, když už jsme ten Korespondenční Seminář z Programování.
Abychom se vyhnuli ovlivňování pravidel, zpracovávejme je v jiném pořadí, než je vypisuje odevzdávátko. Totiž takovém, kde se nemusíme k již splněným pravidlům vracet:
Zakázané písmeno
Než vůbec začneme cokoliv přidávat, uvědomme si, že do hesla vůbec nemůžeme přidat jedno písmeno. Nicméně zakázané písmeno nebude takové, bez kterého by úloha nešla vyřešit. (Tedy z města na souřadnicích,IX z
římské minuty a z, pokud hrošík pocházel ze ztka.
) U všech ostatních pravidel existují alespoň dvě možnosti bez společných písmen.
Sponzor
Zde stačilo najít jednoho z našich sponzorů na stránkách. Sponzoři byli např.MFF, MSMT, RSJ nebo JetBrains. Někteří sice obsahují
velké písmeno, které porušuje pravidlo s římskými minutami, nicméně šlo je celé
napsat malými písmeny.
Město na souřadnicích
Tady se jedná o pravidlo na hledání vhodné knihovny. Rychlé vyhledávání najde přesně to, co bychom potřebovali.Úloha s hrošíkem
Pravidlo na scrapování webu. Nicméně ve struktuře webu obrázek hrošíka není syn nadpisu dané úlohy. Ale to vyřešíme tak, že budeme tagy procházet popořadě a pamatovat si, ve které úloze aktuálně jsme.Římská minuta
Prvním nápadem by mohlo být doplnit správný početI.
Ale pro vyšší počty minut to rychle selže, protože atomové číslo jódu je 53
a cílový součet atomových čísel je okolo 750. Ale stačí použít přidat
správný počet X a I, což funguje spolehlivě.
Poznámka na okraj: Tohle se hodí dělat až po časově náročném pravidle s hrošíkem, protože trvá dlouho a mezitím se může změnit minuta.
Součet atomových čísel
Začněme tím, že římská minuta a město nás může donutit již nějaké prvky přidat. Proto si nejdřív spočítejme rozdíl aktuálního a cílového součtu.
Pokud zakázané písmeno není H, tak přidejme vodík.
Jinak předpokládejme, že rozdíl je alespoň alespoň 3. Heslo doplňme
nejdřív Li, Be nebo B (s atomovými čísly 3, 4 a 5),
podle zbytku po dělení třemi. Teď je rozdíl dělitelný třemi a můžeme
přidat správný počet lithia.
Balancování velkých a malých písmen
Zde stačí spočítat častější velikost písmen a doplnit písmenem jiným od zakázaného.Malé, velké písmeno, číslo
Malé a velké písmeno už určitě máme kvůli předchozím bodům, přidejme do hesla číslici.Prvočíselná délka
Tady si najdeme nejmenší prvočíslo větší rovno než délka hesla. To můžeme dělat ověřováním podle definice, nebo Eratosthenovým sítem. Poté doplníme číslicemi tak, aby délka hesla byla prvočíselná.Pro potvrzení zadej heslo znovu:
Poslední pravidlo bylo hlavně trikové a stačilo heslo vypsat dvakrát za sebou na různé řádky. 36-4-S Nechme stromy růst (Zadání)
36-4-S Nechme stromy růst (Zadání)
První dvě úlohy byly více programovací a myslíme, že implementace byla víceméně přímočará. Kromě samotného textu seriálu byl v šabloně i obrovský komentář, jak jednotlivé části naimplementovat, tedy doufáme, že nikdo neměl s implementací problém.
Pár lidí se ptalo na rychlost a samozřejmě jsme
brali všechna správná řešení bez ohledu na rychlost.
Občas je zrychlení programu pomocí numpy dost znatelné
a my při zadávání úlohy jsme ani nezkoušeli, jak moc pomalé
je řešení bez numpy.
Vzorové řešení rozhodovacího stromu (Python 3)
Vzorové řešení náhodného lesu (Python 3)
Soutěžní úloha
Očekávané řešení na projití baseliny bylo použití modelu RandomForestClassifier
a pohrát si s hyperparametry pro dosažení co nejlepších výsledků.
Důležité se nebát počtu stromů, protože jak jednotlivé stromy
jsou většinou dost slabé, tak je potřeba jich mít dostatečně mnoho, aby se výsledky zlepšily.
Pro představu, při testování jsme používali stovky až tisícovky stromů.
U této úlohy dost dobře funguje model ExtraTreesClassifier, který i bez
libovolných nastavování parametrů dokáže dát přes 97 %.
Trochu k údivu bylo nakonec zjištění, že nejlepší lidi v soutěží použili logistickou regresi s multiclass klasifikací one-over-rest či softmax (multinomial logistic regression). Tyto dobré výsledky těchto modelů jsou dost pravděpodobně způsobeny tím, že data byly z původního datasetu upravena (každý blok 8×8 pixelů byl nahrazen za jednou hodnotu). Kdybychom opravdu dostali jednotlivé pixely, výsledky těchto modelů bychom očekávali mnohem horší. To kvůli tomu, že jednotlivé pixely vůbec nic neříkají o celkovém obrazu.
 36-4-X1 Počet koček (Zadání)
36-4-X1 Počet koček (Zadání)
Kočka klasická
Nejprve si rozmyslíme, jak se hledá kočka klasická, tedy řetězec KOCKA.
Budeme procházet textem zleva doprava a počítat, kolikrát už jsme
potkali jednotlivé prefixy kočky. Budeme si tedy udržovat počítadla
pK, pKO, pKOC až pKOCKA.
Kdykoliv narazíme na nový znak textu, provedeme:
K: objevíme jednak nový výskyt prefixuK, jednak každý předchozí výskytKOCrozšíříme naKOCK. V řeči počítadel tedy pK += 1 a pKOCK += pKOC.O: z každéhoKvznikne novéKO, tedy pKO += pK.C: z každéhoKOvznikne novéKOC, tedy pKOC += pKO.A: z každéhoKOCKvznikne celéKOCKA, čili pKOCKA += pKOCK.- jiné písmeno: počítadla se nezmění.
Teď se nabízí říci si, že se přeci pokaždé jedná o nějaké lineární transformace vektoru počítadel (pK,… ,pKOCKA), sáhnout po loňském seriálu o lineární algebře a transformace elegantně popsat násobením matic.
Jenže ouha: při výskytu K přičítáme jedničku, což není lineární,
nýbrž afinní transformace (stejně jako je v geometrii posunutí). Mohli bychom
reprezentaci maticemi rozšířit i na afinní zobrazení, ale místo toho si
pomůžeme jednoduchým trikem: Představíme si, že na začátku kočky je nějaký
speciální znak ♥, který se vyskytuje těsně před začátkem textu a pak
už nikde jinde. Tím pádem p♥ bude vždy 1 a za každé K
provedeme pK += p♥.
Teď už můžeme reakce na jednotlivé znaky textu popsat maticemi:
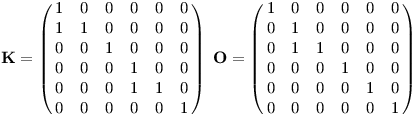
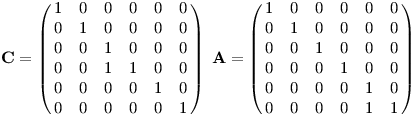
K pak (sloupcový) vektor počítadel násobíme maticí K zleva:
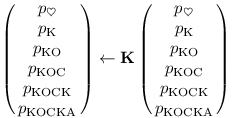
Textu délky T tedy můžeme přiřadit nějakou posloupnost matic M1, …, MT a bude platit:
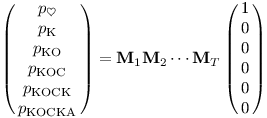
Kočka obecná
Pro obecnou kočku délky K sestrojíme matice podobně. Budou to matice tvaru (K+1) ×(K+1), jejichž indexy řádků a sloupců budou odpovídat prefixům kočky; první řádek a sloupec odpovídají prázdnému prefixu, tedy virtuálnímu znaku ♥. Matice pro znak z bude mít jedničky na hlavní diagonále a kdykoliv se dá (i-1)-ní prefix rozšířit na i-tý přidáním z, umístíme další jedničku na pozici (i,i-1). Pokud se z vůbec nevyskytne v kočce, dává toto pravidlo jednotkovou matici.
Intervalové stromy
K vyřešení úlohy nám teď stačí vybudovat datovou strukturu pro posloupnost matic, která bude umět pro libovolný úsek posloupnosti rychle spočítat součin matic v úseku.
Na to se dá použít například intervalový strom, jehož listy budou odpovídat prvkům posloupnosti a každý vnitřní vrchol bude obsahovat součin matic ve svých dětech. (Oproti stromům nad posloupnostmi čísel si musíme dávat pozor na to, že násobení matic není komutativní. To ale intervalovému stromu nevadí, potřebuje pouze asociativitu a tu násobení matic splňuje.)
Strom vybudujeme pomocí O(T) násobení matic. Každé z nich počítáme v čase O(K3), což bychom případně mohli zrychlit Strassenovým algoritmem, ale jelikož je K mnohem menší než T, nebudeme tento krok dál optimalizovat. Vytvořit celý strom nám tedy trvá O(K3T).
Intervalový dotaz potřebuje projít cestu z listů ohraničujících interval do jejich nejbližšího společného předka a v každém vrcholu provést O(1) násobení matic. Cesta má logaritmickou délku, takže celý dotaz trvá O(K3 log T).
Ze součinu matic v intervalu pak dostaneme hledaný počet koček jedním dalším násobením matic, což asymptotickou složitost nezhorší.
Statická struktura
Zkusme se nad problémem zamyslet abstraktněji: máme nějakou posloupnost prvků x1,… ,xN a nějakou asociativní operaci *, které budeme říkat násobení. Chceme statickou datovou strukturu, která umí odpovídat na dotazy xi*xi+1*… *xj. Při analýze časové složitosti budeme zatím předpokládat, že * umíme spočítat v konstantním čase.
Intervalové stromy náš obecný problém řeší, ale dokázaly by fungovat i dynamicky – přepočítávat strukturu při změnách prvků posloupnosti. To je zbytečně silné: nám stačí statická struktura, a ta opravdu může být efektivnější.
Posloupnost rozdělíme v polovině a rozlišíme dva druhy dotazů: jedny kříží polovinu (polovina je obsažena uvnitř intervalu), druhé nekříží. Křížící dotazy vyřídíme jednoduše: pro levou polovinu si předpočítáme suffixové součiny, pro pravou polovinu prefixové. Každý křížící dotaz pak získáme vynásobením suffixového součinu s prefixovým. Co s nekřížícími dotazy? Vybudujeme datové struktury stejného typu zvlášť pro levou a pro pravou polovinu.
Čas potřebný na vybudování struktury velikosti N můžeme vyjádřit rekurentně:
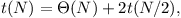
Jak vyhodnotíme dotaz: pokud je křížící, zvládneme to v čase O(1) kombinací předpočítaného suffixu s prefixem. Je-li nekřížící, předáme ho podstruktuře pro příslušnou polovinu. K předání podstruktuře může ovšem dojít až log N-krát, což by nám kazilo složitost. Zde pomůže spočítat, kolik nejvyšších bitů má společných začátek a konec intervalu – to nám řekne hloubku zanoření a hodnota těchto bitů identifikuje, ve které podstruktuře této hloubky máme hledat. Společné nejvyšší bity dvou čísel lze spočítat v konstantním čase předpočítanou tabulkou, kterou budeme indexovat binárním xorem obou čísel. Takto dokážeme na každý dotaz odpovědět v konstantním čase.
Při použití této datové struktury k počítání koček budeme ještě muset vynásobit složitost operací složitostí násobení matic O(K3). Vybudování struktury tedy potrvá O(K3T log T) a dotaz poběží v čase O(K3).
Dodejme ještě, že podobnou dekompozici na podstruktury jde provést i obecněji a zrychlovat předvýpočet za cenu zpomalování dotazu. Obě složitosti se vyrovnají na předvýpočtu v čase O(Nα(N)) a dotazu v O(α(N)), kde α je inverzní Ackermannova funkce, kterou jste možná potkali v analýze Union-Findu. My si nicméně detaily odpustíme, protože následující řešení bude ještě lepší.
Prefixové součty
Úplně nejjednodušší datovou strukturou pro vyhodnocování operace přes interval jsou staré dobré prefixové součty. Proč se vlastně nedají použít v této úloze? Zkusme to.
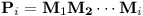
| -1 |
| i-1 |
S tím nastanou dva problémy. Tím méně vážným je, že násobení matic nekomutuje. Rozmyslíme-li si ovšem, že platí (AB)-1 = B-1A-1, můžeme ověřit, že
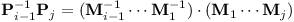
| -1 |
| i |
| -1 |
| i |
Všechny matice Mi jsou dolní trojúhelníkové a determinant trojúhelníkové matice je (triviálně podle definice) roven součinu prvků na hlavní diagonále. Naše matice tedy mají determinant rovný jedné, takže jsou regulární a mají inverzi.
Nejen to, dokonce se jejich inverze dají jednoduše vyjádřit. Představme si nějakou „kočkovitou“ matici, třeba:

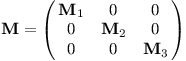
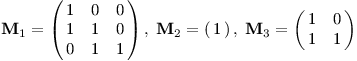
Teď se bude hodit, že násobíme-li dvě matice složené z bloků odpovídajících velikostí, stačí je násobit po blocích – první blok s prvním, druhý s druhým a tak dále. Proto i inverzi matice je možné provádět po blocích.
Zbývá tedy ukázat, jak vypadá inverze jednoho bloku. Řešíme maticovou rovnici typu
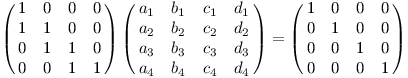
Pro první sloupec to dopadne následovně:
- První rovnice: a1 = 1.
- Druhá rovnice: a1 + a2 = 0, z čehož a2 = -1.
- Třetí rovnice: a2 + a3 = 0, takže a3 = 1.
- Čtvrtá rovnice: a3 + a4 = 0, a proto a4 = -1.
V druhém sloupci získáme:
- První rovnice: b1 = 0.
- Druhá rovnice: b1 + b2 = 1, z čehož b2 = 1.
- Třetí rovnice: b2 + b3 = 0, takže b3 = -1.
- Čtvrtá rovnice: b3 + b4 = 0, a proto b4 = 1.
Celkově to dopadne takto:
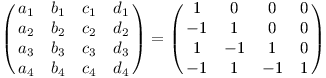
Pro blok velikosti k×k bude mít inverze v i-tém sloupci nejprve i-1 nul a pak se budou střídat jedničky s minus jedničkami. Nebo to můžeme popsat tak, že na hlavní diagonále jedničky a pod diagonálou šachovnice z plus a minus jedniček. (To je v souladu s tím, že inverze dolní trojúhelníkové matice je zase dolní trojúhelníková.)
| -1 |
| i |
Předvýpočet tedy provede O(T) maticových součinů, takže potrvá O(K3 T). Dotaz pak obnáší O(1) násobení matic v celkovém čase O(K3). Datová struktura si pamatuje O(T) matic, takže zabere prostor O(K2 T).
Princip inkluze a exkluze
Ještě si předvedeme jedno řešení s hezkou časovou složitostí. Inspirujeme se principem a exkluze (zahrnutí a vyloučení) známým z kombinatoriky. Ve vší obecnosti by se dal formulovat tak, že když započítáme něco navíc, následně to odečteme, čímž jsme zase možná odečetli něco navíc, to přičteme atd. Prefixové součty jsou triviálním příkladem takového výpočtu, teď se bude hodit jeden trochu méně triviální.
Nechť P(a,b,i,j) říká, kolikrát se v podřetězci textu na indexech a,… ,b-1 vyskytuje podřetězec kočky na indexech i,… ,j-1. Naše úloha po nás tedy chce počítat P(a,b,0,K).
Uvažujme takto: předpočítáme si P(0,b,0,K) – to je počet koček v prvních b znacích textu. Od toho odečteme předpočítané P(0,a,0,K) – počet koček v prvních a znacích. Teď máme správně započítané všechny kočky od a do b, ale navíc i kočky, které kříží a-tý znak. Tak je odpočítáme: koček, které mají nalevo od a svůj prefix délky ℓ a mezi a a b zbytek, je P(0,a,0,ℓ) ·P(a,b,ℓ,K). Sečtením přes všechna ℓ dostaneme:
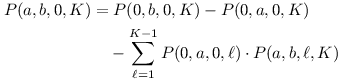
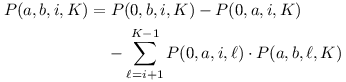
Nakonec popíšeme předvýpočet. Budeme počítat všechna P(0,b,i,j) indukcí podle b (postupným rozšiřováním textu). Inspirováni úvahou o kočce klasické z úvodu, provedeme to takto:
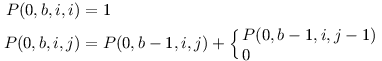
Předvýpočet tedy poběží v čase O(K2T) a na každý dotaz odpovíme v čase O(K2). Datová struktura zabere prostor O(K2T).