První série třicátého šestého ročníku KSP
Celý leták v PDF.
Řešení úloh
- 36-1-1: Strom v zrcadle
- 36-1-2: Taneční
- 36-1-3: Výšlap
- 36-1-4: Mediánový filtr
- 36-1-5: Nejlepší programovací jazyk, část I.
- 36-1-S: Seznámení se s lineární regresí
- 36-1-X1: Mezigalaktická kandidátka
 36-1-1 Strom v zrcadle (Zadání)
36-1-1 Strom v zrcadle (Zadání)
Máme rozhodnout, zda je zadaný strom symetrický. Tedy jestli když prohodíme pravého a levého syna každého vrcholu, dostaneme tvarem i hodnotami ve vrcholech stejný strom jako na začátku. Dále nesmíme zapomínat, že zadaný strom nemůžeme nikam kopírovat, protože můžeme použít pouze konstantní množství paměti navíc.

Pro rozhodování o symetričnosti si pořídíme dva ukazatele. Jeden nazveme hlavní, druhý bude kontrolní. Hlavním ukazatelem budeme procházet vrcholy v pořadí, jako bychom strom prohledávali do hloubky. Kontrolním ukazatelem budeme postupovat symetricky opačně. Když tedy hlavním půjdeme do levého syna, kontrolním se přesuneme do pravého syna, a naopak. Na začátku jsou oba ukazatele v kořeni. Mějme na paměti, že si nemusíme (dokonce ani nemůžeme) udržovat zásobník rekurze, neboť v každém vrcholu poznáme, kam se máme vydat dál, podle toho, odkud jsme do něj přišli. Všimněme si, že kontrolní ukazatel míří vždy na vrchol, na který se ozrcadlí vrchol hlavního ukazatele. Dokážeme tedy separátně o každém vrcholu rozhodnout, jestli má správný obraz.
Když hlavním ukazatelem procházíme strom, může se stát, že po kontrolním ukazateli budeme požadovat přesun na neexistujícího syna. To ale také znamená, že strom není symetrický – nějaký prvek by po ozrcadlení neměl obraz.
Jestliže projdeme celý strom, aniž by nastala nějaká z podmínek přerušení, máme vyhráno. Nyní už musí být strom symetrický. Prohledáváním do hloubky jsme jej prošli celý a pro každý vrchol zkontrolovali, že se shoduje jeho hodnota s hodnotou jeho obrazu.
Každým ze dvou ukazatelů jsme jednou prošli celý strom. Časovou složitost tedy dostáváme O(N). Při průchodu stromem jsme alokovali pouze konstantní množství proměnných, paměťová složitost je proto O(1).
 36-1-2 Taneční (Zadání)
36-1-2 Taneční (Zadání)
Označme jako P[i] pozici pána zvoleného i-tou dámou. Jak pro dvě dámy poznat, zda se jejich dráhy kříží? Nahlédneme, že dráhy i-té a j-té dámy se nekříží, právě když P[i] < P[j]. To lze zobecnit: dráhy dam na pozicích i1, … , ik se nekříží, právě když P[i1] < ...< P[ik], tedy je-li podposloupnost P[i1], … , P[ik] rostoucí. Vskutku: pokud pro nějaké ℓ neplatí P[iℓ] < P[iℓ+ 1], pak se tyto dvě dámy nutně kříží, a naopak, pokud pozice pánů rostou s pozicemi vybraných dam, pak je nemožné, aby se libovolné dvě dráhy zkřížily.
Nemusíme tedy vůbec řešit nějaké křížení dam, stačí nám nalézt co nejdelší podposloupnost pole P, která je rostoucí. Jinými slovy, právě jsme úlohu převedli na problém hledání nejdelší rostoucí podposloupnosti (NRP). To je známý problém, který umíme řešit v O(N log N) času a O(N) paměti, a ve zbytku řešení si ukážeme, jak na to.
NRP budeme hledat pomocí dynamického programování. Pokud jste o něm ještě neslyšeli, můžete nakouknout do naší kuchařky – ale nebojte, řešení by mělo být pochopitelné i bez toho. Jeho obecný princip je prostý: abychom spočetli řešení celého problému, budeme počítat řešení malých, ale čím dál větších, podproblémů, ze kterých pak nakonec celé řešení poskládáme. Pro náš problém se konkrétně nabízí spočítat nejdříve NRP pro první prvek, pak pro první dva prvky, …, až spočteme NRP celého P, přičemž se vždy k dosavadnímu NRP v každém kroku pokoušíme přidat aktuální prvek. To je úvaha správným směrem, ale sama o sobě nefunguje: důkazem budiž P = [4, 5, 1, 2, 3], kde nesprávně odpovíme [4, 5]. Potíž je v tom, že si toho počítáme příliš málo a neumíme pak z odpovědí pro menší problémy počítat odpovědi pro problémy větší. Hladově se pak zafixujeme na nějakou podposloupnost, která se ze začátku jeví optimální, ale nakonec není.
Pojďme to napravit. Místo, abychom si udržovali jen průběžnou NRP, budeme si rostoucích podposloupností (RP) udržovat více. Konkrétně si pro každé k budeme udržovat, jestli z dosavadních prvků umíme vyrobit RP délky k, a pokud ano, tak na jakou nejnižší hodnotou taková RP může končit. Formálně tuto hodnotu označíme A[i][k], kde i je počet zatím zpracovaných prvků P a k kýžená délka RP. Snadno nahlédneme, že finální délku NRP na konci získáme z A[N] tak, že se podíváme, pro jaké největší k ještě A[N][k] existuje.
Zbývá popsat, jak pomocí A[i - 1] a aktuálního prvku P[i] spočítat A[i][k]. K tomu stačí rozlišit dvě možnosti, jak taková RP může vypadat, a vzít z nich tu lepší: Buď nejlepší RP reprezentovaná v A[i][k] má končit na P[i], nebo nikoliv. Pokud RP na P[i] nemá končit, pak nutně A[i][k] = A[i - 1][k], jelikož nově přidaný prvek v RP nijak nevyužíváme. Pokud naopak RP na P[i] končit má, pak A[i][k] = P[i]. Tuto možnost ale smíme použít pouze v případě, že nějaká taková RP vskutku existuje – to jest, pokud můžeme vzít nějakou podposloupnost délky k - 1 a za ni P[i] nalepit. To ověříme snadno – prostě P[i] porovnáme s A[i - 1][k - 1], a pokud je P[i] menší, znamená to, že ani za co nejníže končící RP délky k - 1 ho nalepit nejde, a tudíž ho použít nesmíme.
Aby měl náš algoritmus kde začít, inicializujeme A[0][0] na minus nekonečno. Tuto prázdnou posloupnost půjde rozšířit každým prvkem z P.
Pro důkaz správnosti stačí nahlédnout, že jsou-li hodnoty A[i - 1] spočítány správně, pak i každé A[i][k] bude správně. Spokojíme se s neformálními úvahami z předchozího odstavce, pro formální důkaz bychom měli důkladněji ověřit, že každá potenciálně lepší RP bude pokrytá jednou ze dvou rozebíraných možností.
Časová složitost tohoto řešení je O(NK), kde K ≤ N je délka NRP. Paměťová složitost je též O(NK), ale můžeme ji zlepšit na O(K), budeme-li si místo celého A pamatovat vždy jen dva poslední řádky.
Zrychlujeme
K rychlejšímu řešení nás dovede pozorování: Umíme něco říct o vzájemném vztahu A[i][0], A[i][1], … , A[i][k]? Jinými slovy, když z nějakého pole vybíráme stále delší a delší RP, co můžeme říct o nejnižších dosažitelných hodnotách posledních prvků? Nahlédneme, že musejí růst: Máme-li RP odpovídající A[i][k], můžeme z ní odebrat poslední prvek x, čímž dostaneme nějakou RP délky k - 1, s posledním prvkem y < x. Teď sice nevíme, jaká optimální RP je v A[i][k - 1], ale jelikož to je optimální RP délky k - 1 a my jsme právě vyrobili nějakou RP délky k - 1, musí nutně platit, že A[i][k - 1] ≤ y < x = A[i][k].
Učiníme ještě druhé pozorování: A[i] se od A[i - 1] liší nejvýše jedním prvkem. Každý odlišný prvek v A[i] totiž musí mít hodnotu rovnou P[i], a ta se v ostře rostoucí posloupnosti A[i] může objevit nejvýše jednou.
Konkrétně, pokud jsme změnili prvek A[i][k], pak určitě P[i] < A[i - 1][k] (jinak bychom v posloupnosti nechali A[i - 1][k], protože je lepší) a zároveň P[i] > A[i - 1][k - 1] (jinak P[i] nesmíme použít). To nám ale dává návod na rychlý algoritmus: místo, abychom A[i] vždy v O(N) počítali z A[i - 1], stačí nejprve binárním vyhledáváním najít správné k, A[i - 1][k] upravit, a pak A[i - 1] prostě prohlásit za A[i]. Nemusíme si tedy vůbec počítat dvojrozměrnou tabulku, ale bude nám stačit obyčejné pole, které pod rukama měníme.
Časová složitost takového řešení je O(N log N), paměťová O(N). Na závěr si ještě rozmysleme, jak kromě délky NRP i tuto podposloupnost vypsat. K tomu si stačí v každém kroku poznačit, jakou hodnotu jsme právě upravili. Po spočtení NRP pak tento záznam úprav můžeme pozpátku projít a vypsat ta i, ve kterých jsme naši budoucí NRP prodlužovali. Pro detaily nahlédněte do vzorového řešení.
 36-1-3 Výšlap (Zadání)
36-1-3 Výšlap (Zadání)
Cesta vzhůru
Nejprve vyřešíme o něco jednodušší úlohu. Bude nás prozatím zajímat jen cesta nahoru, chceme tedy přijít na to, kam můžeme ze startu co nejdelší cestou vylézt.
Pořídíme si tedy tabulku, do které budeme chtít pro každé políčko zapsat, jak dlouhá je nejdelší cesta ze startu do něj, nebo si tam poznamenat, že tam žádná cesta nevede. Vzdálenost startu je zjevně jedna.
Spočítat jednu chybějící hodnotu této tabulky zvládneme snadno: Do nějakého políčka můžeme dojít tak, že nejprve dojdeme do níže položeného sousedního políčka, a pak uděláme jeden další krok. Vzdálenost nějakého políčka tedy bude o jedna větší, než největší vzdálenost všech jeho níže položených sousedů. Pokud políčko nemá níže položené sousedy, do kterých se dá dojít, tak se do něj také nedá dojít.
Můžeme si všimnout, že na vzdálenost nějakého políčka nemají vliv žádná políčka, co jsou položena stejně vysoko či výše. Stačí nám tedy projít políčka v pořadí od nejnižšího po nejvyšší a pro každé z nich rychle spočítat jeho vzdálenost.
Co kdybychom chtěli cestu do nějakého políčka vypsat? Jednou možností by bylo si ke každému dosažitelnému políčku poznamenat šipku ukazující tím směrem, ze kterého do něj vede nejdelší cesta. Poté bychom mohli snadno cestu vypsat procházením z cíle do startu po těchto šipkách.
Existuje ale i snazší varianta: Víme, že každé dosažitelné políčko kromě startu sousedí s políčkem s o jedna menší vzdáleností. Pokud začneme v cíli a budeme se dokola přesouvat na níže položené políčko s o jedna menší vzdáleností, tak nutně dojdeme do startu, a to po přesně tak dlouhé cestě, jaká je vzdálenost cíle.
Celá cesta
Jak vyřešit celou úlohu a najít nejdelší výšlap? Podle zadání se může cesta nahoru a cesta dolů libovolně křížit. Nejdelší výšlap, který má nejvyšší bod v nějakém políčku, se tedy bude skládat z nejdelší cesty vzhůru ze startu do toho políčka a nejdelší cesty dolů z tohoto políčka do cíle. Nejdelší cestu ze startu do všech políček už najít umíme. Nejdelší cesta dolů do cíle je jen cesta nahoru z cíle, ale pozpátku. Pro každé políčko tedy určíme délku nejdelší cesty do něj ze startu i z cíle a vybereme to, kde je součet těchto délek co největší. V případě rovnosti vybereme to nejvýše položené.
Vypsat výšlap pak zvládneme snadno: Nejprve vypíšeme cestu ze startu a potom vypíšeme cestu z cíle pozpátku. Jen si musíme dát pozor, abychom nevypsali nejvyšší bod dvakrát.
Časová složitost tohoto řešení je O(RS log(RS)), protože musíme seřadit políčka podle výšky. Všechny ostatní části algoritmu běží v O(RS). Paměťová složitost tohoto algoritmu bude O(RS).
Rychlejší řešení
Popsaný algoritmus sice stačí pro získání plného počtu bodů, ale je možné úlohu vyřešit i o něco rychleji.
Abychom náš algoritmus urychlili, musíme se vyhnout třídění políček podle výšky. Uvědomíme si, že abychom mohli spočítat vzdálenost nějakého políčka, tak nemusíme mít spočítané vzdálenosti všech níže položených, ale stačí mít spočítané vzdálenosti všech níže položených sousedů.
Budeme si o každém políčku pamatovat, jestli jsme už jeho vzdálenost spočítali. Dále si vytvoříme frontu, ve které budou všechna políčka, jejichž vzdálenost už spočítat můžeme. Na začátku do fronty dáme všechna políčka, která nemají žádné níže položené sousedy.
Poté budeme opakovaně brát políčka z fronty a počítat jejich vzdálenost. Po spočítání vzdálenosti nějakého políčka se podíváme na všechny jeho sousedy a zjistíme, jestli už můžeme spočítat jejich vzdálenost, tj. zda jsme spočítali vzdálenost všech jejich níže položených sousedů. Pokud tomu tak je, tak daného souseda přidáme do fronty. Jakmile se fronta vyprázdní, tak jsme spočítali vzdálenost všech políček.
Tím úlohu vyřešíme v čase O(RS), což je zajisté optimální, protože musíme přečíst celý vstup. Paměťová složitost upraveného algoritmu bude také O(RS).
 36-1-4 Mediánový filtr (Zadání)
36-1-4 Mediánový filtr (Zadání)
Naivní přístup k řešení problému by byl spočítat mediánový filtr pro každý pixel v obrázku N×N. To by znamenalo, že bychom pro N2 pixelů museli pokaždé od začátku spočítat medián ve čtverci o K2 bodech. Na tomto řešení si můžeme všimnout, že při počítání mediánových filtrů dvou po sobě jdoucích pixelů jsme pracovali s velkým množstvím stejných čísel. Mohli bychom najít řešení, které by nám umožnilo tu samou práci vykonávat jen jednou a šetřit tak časem.
Pro hodnoty ve čtvercích okolo pixelů si budeme udržovat binární vyhledávací strom. Jak budeme postupně procházet všechny pixely obrázku, při každém posunutí ze stromu odstraníme hodnoty pixelů, které už v novém čtverci nejsou, a naopak přidáme hodnoty těch, které byly nově vybrány. Pojďme se na tento přístup podívat detailněji.
Hledání mediánu
Medián je hodnota, která dělí řadu vzestupně řazených prvků na dvě stejně početné poloviny. Jinak řečeno, medián se nachází uprostřed seřazené posloupnosti, ze které medián vybíráme.
Při počítání mediánového filtru pro dané políčko máme ve stromu H hodnot pixelů okolo (většinou bude H = K2, ale na krajích obrázku to bude méně). Pokud budeme umět najít prvek na indexu M v seřazené posloupnosti, zvládneme snadno najít i medián. Pro liché H zvolíme M = (H - 1) / 2 a tento prvek vrátíme jako medián. Pro sudé H najdeme prvky na indexech H / 2 - 1 a M = H / 2 a vrátíme jejich aritmetický průměr.
Abychom mohli takovýto prvek v našem stromu najít, musíme si u každého prvku udržovat velikost jeho levého podstromu (to lze dělat jednoduše při každém vložení či odstranění prvku).
Při hledání samotném budeme procházet strom a udržovat si proměnnou i, ve které si budeme počítat, kolik je vrcholů vlevo od aktuálního, tedy na jakém indexu by skončil aktuální vrchol v poli s hodnotami ze stromu. Začneme v kořeni a nastavíme i na velikost levého podstromu. Všechny prvky levého podstromu jsou totiž menší než aktuální vrchol.
V každém vrcholu porovnáme aktuální pozici i a M. Pokud jsou si rovny, našli jsme hledaný prvek a můžeme skončit. Pokud je i > M, hledaný prvek se nachází v levém podstromu, sestoupíme tedy do levého syna. Pokud je i < M, aktuální vrchol a celý jeho levý podstrom jsou menší než hledaný prvek, proto sestoupíme do pravého syna.
Při sestoupení musíme upravit i. V případě i > M odečteme velikost levého podstromu aktuálního vrcholu a přičteme velikost levého podstromu vrcholu, kam jsme sestoupili. V případě i < M přičteme jedna za aktuální vrchol a poté přičteme velikost levého podstromu vrcholu, do kterého jsme sestoupili.
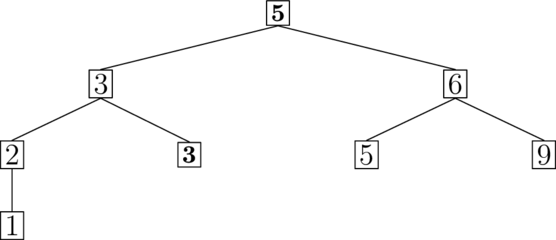
V obrázku výše jsme jako prostřední hodnoty nalezli čísla 3 a 5. Mediánem hodnot tohoto stromu je číslo 4.
Složitost
Náš strom bude vždy obsahovat nejvýše K2 prvků. Při posunutí o jeden pixel v obrázku musíme vždy nejvýše K hodnot smazat a K hodnot vložit dovnitř. Vkládání a mazání prvků binárního vyhledávacího stromu velikosti K2 má složitost O(log K2), což lze upravit na O(log K) a jedno posunutí bude mít tedy složitost O(K log K). Samotné hledání mediánu je taktéž logaritmické, tudíž se stále vejde pod téže časovou složitost. Tuto operaci musíme provést pro N2 pixelů, celková časová složitost je tedy O(N2K log K).
Pokud předpokládáme, že máme celý obrázek již načtený v paměti, musíme si navíc udržovat jen vyhledávací strom o maximální velikosti K2. Paměťová složitost je tedy O(K2).
Všimněme si ještě, že jsme v odvozování složitosti předpokládali, že náš strom má logaritmickou hloubku. To se nám nemusí vždy povést a je tedy důležité strom chytře vyvažovat tak, abychom se stále vešli do námi zvolené horní hranice časové složitosti. Pro to můžeme např. využít AVL strom popsaný v kuchařkách.
 36-1-5 Nejlepší programovací jazyk, část I. (Zadání)
36-1-5 Nejlepší programovací jazyk, část I. (Zadání)
Děkujeme za vaše originální instrukce.
 36-1-S Seznámení se s lineární regresí (Zadání)
36-1-S Seznámení se s lineární regresí (Zadání)
Doplnění derivace
Trochu se vrátíme k derivacím, protože jsme zapomněli zmínit, jak se derivuje součin. Občas jste se potýkali s tím, jak se zderivuje x1,2 ·w2 nebo obecně a ·w2, kde a je libovolná konstanta např. πe.
V obecném případě se derivace součinu f(x) ·g(x) rovná f'(x) ·g(x) + f(x) ·g'(x). Nám však postačí jednodušší pravidlo, neboť násobíme pouze konstantou. V takovém případě je výpočet jednoduchý: konstantu lze vytknout před derivaci, tedy derivace a ·f(x) je a ·f'(x). Toto pravidlo jsme nezmiňovali, protože jsme jej brali jako samozřejmost. Můžete si jej ověřit pomocí obecného vzorce pro derivaci součinu.
První 3 úlohy byly zaměřené na implementaci teorie ze seriálu. V našem vzorovém řešení máme
naimplementované úlohy tak, jak jsme je od vás očekávali (jen pomocí Pythonu), tak i pomocí
knihovny numpy, kde výpočty jsou vektorizované.
Úkol 4 – Těžký bonusový úkol: Explicitní výpočet vah [0b]:
Tento úkol nebyl vůbec komplikovaný. Úkol byl převést tento zápis na jeho „zvektorizovanou“ formu, tedy aby zápis používal maticové operace a počítal vše „naráz“:
| p1 ·x1,1 + …+ pn ·xn,1 = t1 ·x1,1 + …+ tn ·xn,1 |
| p1 ·x1,2 + …+ pn ·xn,2 = t1 ·x1,2 + …+ tn ·xn,2 |
| ⋮ |
kde pi jsou predikce našeho modelu, ti jsou správné výstupy a xi,j znamená j-tá fearura i-tého data. Nebo ještě o něco lepší zápis:
| (p1 - t1) ·x1,1 + …+ (pn - tn) ·xn,1 = 0 |
| (p1 - t1) ·x1,2 + …+ (pn - tn) ·xn,2 = 0 |
| ⋮ |
Nechť predikce a targety (správné výstupy) jsou vektory p a t a X je matice, kde i-tý řádek je i-té dato. Odečíst dva vektory není problém, teď jen potřebujeme daný rozdíl vektorově pronásobit s maticí X. Vidíme, že v první rovnici používáme jen první featury dat, v druhé rovnici jen druhé featury atd. Když matici transponujeme a vynásobíme zprava rozdílem vektorů, tak dostaneme požadovaný výsledek.
Nyní ještě budeme trochu upravovat. Jak vypočítáme predikce? Pronásobíme váhy s featurami a sečteme, tedy p = X ·w. Dosadíme do předchozí rovnice a dostaneme:
Teď targety dáme na pravou stranu rovnice:
A nyní zbývá poslední krok, vynásobit rovnice zleva maticí inverzní k X⊤·X:
Poslední krok můžeme udělat, protože matice X⊤·X je čtvercová, ale nikdo nám nezaručuje, že tato matice bude invertovatelná (může se jednat o singulární matici). Na běžných datech tato situace spíše nenastane, ale dá se řešit pomocí L2 regularizace, kde je dokázané, že tato matice bude vždy invertovatelná. Povídání o L2 regularizaci naleznete v 2. díle seriálu.
Úkol 5 – Prozkoumáváme scikit-learn [5b]:
Tento úkol byl zaměřený, abyste se trochu seznámili s knihovnou scikit-learn.
Nejdříve bylo potřeba použít funkci train_test_split, která rozdělí data na trénovací a testovací.
Této funkci je potřeba předávat naráz data i targety (správná výstupní data), aby funkce věděla,
že k danému datu patří daný výstup.
import sklearn.datasets
from sklearn.model_selection import train_test_split
# načtení datasetu
diabetes = sklearn.datasets.load_diabetes()
# rozdělení datasetu na trénovací a testovací
X_train, X_test, y_train, y_test = train_test_split(
diabetes.data, diabetes.target, test_size=0.2)
)
Poté jste měli natrénovat a spočítat chybu modelu.
import sklearn.linear_model as lm
import sklearn.metrics
model = lm.LinearRegression()
# natrénování modelu
model.fit(X_train, y_train)
predikce = model.predict(X_test)
# výpočet chyby modelu
mse = sklearn.metrics.mean_squared_error(
y_test, predikce
)
print(mse)
Nakonec jste se měli podívat na jiné metriky určené na úlohu regrese a vybrat si nějakou, která se vám zdála nejvíce vhodná nebo zajímavá. Pro daný dataset dává smysl např. maximální absolutní chyba, protože v lékařství se klade důraz na přesnost. Predikce modelu by se neměli mít velké odchylky od skutečných hodnot.
Zaokrouhlování
Ve strojovém učení se moc nepotkáváme se zaokrouhlováním a moc vám ho nedoporučujeme dělat, pokud nevíte, proč by to mělo pomáhat. Typicky tím můžete zhoršovat model na dané metrice. Pokud chcete zaokrouhlovat nebo jen ořezávat hodnoty, tak vám to doporučujeme dělat po 6.--7. desetinném místě. Rozhodnutí je samozřejmě ale jen na vás.
 36-1-X1 Mezigalaktická kandidátka (Zadání)
36-1-X1 Mezigalaktická kandidátka (Zadání)
Nejprve zavedeme trochu praktičtější terminologii: V posloupnosti n barev z rozsahu 1,… ,k chceme najít nejdelší bílý úsek, což je ten, ve kterém jsou všechny barvy zastoupeny stejným počtem. Zjevně můžeme předpokládat, že k≤ n, protože jinak je bílý jenom prázdný úsek.
Dvě barvy
Nejprve si rozmyslíme, jak se úloha chová pro malé počty barev. Začneme se dvěma. Tehdy stačí jednu barvu považovat za 1 a druhou za -1. Bílé úseky budou přesně ty, které mají nulový součet.
Teď už do toho stačí praštit standardním kladívkem, totiž prefixovými součty. Hledáme nejdelší úsek, který má na začátku stejný prefixový součet jako na konci. Budeme procházet posloupnost od začátku do konce. Pokaždé se podíváme, jestli jsme danou hodnotu prefixového součtu už viděli. Pokud ne, zapamatujeme si, že na této pozici to bylo poprvé. Pokud už ano, zkontrolujeme, zda úsek od prvního výskytu k aktuálnímu není delší než dosavadní maximum.
Potřebujeme tedy slovník, jehož klíče budou prefixové součty a hodnoty budou pozice ve vstupu. Jenže prefixové součty vždy leží v rozsahu -n,… ,n, takže jimi můžeme indexovat pole.
Toto řešení běží v čase O(n) včetně inicializace pole.
Tři barvy
Přidejme barvu. Teď bychom mohli nahradit barvy komplexními třetími odmocninami z jedničky a tím úlohu zase převést na hledání úseku s nulovým součtem. Ale to by jednak znamenalo zacházet s iracionálními čísly, a jednak by to nešlo dále zobecňovat pro počty barev, které nejsou prvočísla.
Místo toho se inspirujeme tím, že v našem řešení pro 2 barvy je prefixový součet roven b1[i] - b2[i], kde bj[i] říká, kolikrát se v úseku od 1 do i vyskytla j-tá barva.
Pro 3 barvy si pořídíme vektor (b1[i] - b2[i], b2[i] - b3[i]). Opět si všimneme, že bílé úseky poznáme podle toho, že končí stejným vektorem jako začaly. (Rovnost v první složce znamená, že barvy 1 přibylo během úseku stejně jako barvy 2, druha složka pak zaručí, že barvy 2 přibylo stejně jako barvy 3.)
Hodila by se nám tedy datová struktura, která si pro každý vektor zapamatuje, kdy jsme ho poprvé viděli. To by mohl být nějaký vyvažovaný vyhledávací strom, což by vedlo na dotaz v čase O(log n) a celé řešení v čase O(n log n). Nebo by to mohla být hešovací tabulka s průměrnou časovou složitostí dotazu O(1), takže by celé řešení běželo průměrně v O(n).
Nám by se ale daleko více líbilo řešení, které by bylo lineární i v nejhorším případě. Všimneme si, že slovníkovou datovou strukturu můžeme jednoduše nahradit tříděním. Ke každému vektoru si poznamenáme pozici ve vstupu. Vektory pak setřídíme lexikograficky, čímž se stejné vektory dostanou k sobě. Postačí tedy v každém bloku stejných vektorů najít první a poslední výskyt. Dvojice čísel z rozsahu -n,… ,n můžeme setřídit dvouprůchodovým přihrádkovým tříděním v lineárním čase. Toto řešení už bude lineární i v nejhorším případě.
Více barev
Předchozí řešení snadno zobecníme pro k>2 barev. Vektory budou (k-1)-složkové a budou obsahovat
Operace s nimi potrvají O(k) a přihrádkové třídění poběží v k-1 průchodech o celkové složitosti O(kn). Taková bude i celková složitost algoritmu.
Rozděl a panuj
K řešení s lepší časovou složitostí pro hodně barev se můžeme dostat například metodou Rozděl a panuj. Úlohu pro k barev budeme předvádět na dvě podúlohy pro k/2 barev. Prvním ⌊k/2⌋ barvám budeme říkat dolní, zbylým ⌈k/2⌉ barvám horní.
Všimneme si, že bílý úsek v k barvách je přesně ten, který splňuje současně tyto tři podmínky:
- Je bílý v dolních barvách (přičemž horní ignorujeme).
- Je bílý v horních barvách (dolní ignorujeme).
- Je v něm stejně první horní barvy jako první dolní.
Abychom na první dvě podmínky mohli snadno použít rekurzi, budeme rekurzivně řešit následující problém: Pozicím ve vstupu chceme přiřadit celočíselné kódy tak, aby bílé úseky byly přesně ty, které na začátku a na konci mají stejný kód. Pro k=2 barev definici kódu splňují prefixové součty, pro k=3 můžeme po setřídění každému bloku stejných vektorů přiřadit unikátní kód.
Pro větší k budeme postupovat takto: Nejprve si necháme zkonstruovat kódy a[i] pro dolní barvy, a to tak, že se zavoláme rekurzivně na posloupnost, z níž jsme odstranili všechny horní barvy. Tím získáme a[i] na pozicích dolních barev; horním zkopírujeme hodnotu od předchozí dolní barvy (pokud žádná předchozí nebyla, použijeme pevně přidělený kód pro 0 výskytů). Obdobně vyrobíme kódy b[i] pro horní barvy.
Třetí podmínku ošetříme pomocí c[i] definovaného jako rozdíl počtu prvků první horní barvy a první dolní na počátečních i pozicích. Všechna c[i] spočítáme v lineárním čase.
Nakonec vytvoříme vektory (a[i], b[i], c[i]), poznamenáme si k nim pozici i a setřídíme je lexikograficky pomocí přihrádkového třídění. Každému souvislému bloku stejných vektorů přiřadíme stejný kód.
Rekurzi ukončíme pro k=1, kde je úloha triviální: všechny pozice dostanou stejný kód.
Jakou časovou složitost toto řešení má? Na problém délky n s k barvami použijeme dvě rekurzivní volání na problémy délek nd a nh (počet prvků dolních a horních barev, přičemž nd + nh = n). Navíc spotřebujeme O(n) času na přihrádkové třídění, přidělování kódů a další režii. Časová složitost tedy splňuje (až na zaokrouhlování) rekurenci
Představme si strom rekurze. Každý vnitřní vrchol má 2 syny s polovičním k, takže existuje log k hladin. Podproblémy na jedné hladině mají součet délek n (každý prvek vstupu patří do právě jednoho z těchto podproblémů), takže režie algoritmu se přes celou hladinu sečte na O(n). Celkem tedy algoritmus běží v čase O(n log k).
Kódování stromečků
Ukážeme ještě jeden přístup, který také vede k efektivnímu řešení pro hodně barev. Prvkům přiřadíme (k-1)-složkové vektory stejně jako v řešení z části „Více barev“. Vektorům budeme chtít zase přiřazovat kódy tak, aby stejné vektory odpovídaly stejným kódům, a budeme hledat nejvzdálenější výskyt stejných kódů. Ovšem kódy budeme vytvářet jinak.
Pro každý vektor vytvoříme úplný binární strom. V jeho listech budou složky vektoru. Pro jednoduchost vektory doplníme nulami na nejbližší vyšší mocninu dvojky K (víme, že k-1≤ K<2(k-1)). Strom tedy bude mít hloubku log K ≤ log k + 1.
Všechny vrcholy stromu opatříme kódy tak, aby pro každý podstrom platilo, že kód v jeho kořeni jednoznačně identifikuje hodnoty v listech. Kód kořene tedy jednoznačně určuje celý vektor.
Kódy vrcholů můžeme počítat od listů ke kořeni. Kód listu bude prostě jeho hodnota. Pokud už známe kódy na i-té hladině (počítáno od kořene) a chceme zakódovat (i-1)-ní hladinu, stačí každému vrcholu přiřadit uspořádanou dvojici kódů synů a pak stejným dvojicím přidělit stejný kód.
Pořídíme si nějakou slovníkovou datovou strukturu, která si pamatuje všechny dvojice, jež jsme zatím potkali, a jejich kódy. Pokaždé, když chceme zakódovat vrchol, zeptáme se datové struktury, a pokud se tam dvojice ještě nevyskytla, přidělíme nový kód a zapíšeme do struktury.
Takto bychom celý strom zakódovali pomocí 2K-1 operací se strukturou, což je příliš. Tak si všimneme, že za každý prvek vstupu se vektor změní v nejvýše dvou složkách (prvek barvy i změní bi-1-bi a bi-bi+1). A po změně jedné složky stačí překódovat cestu z listu do kořene. Celkem tedy stačí 2 log K ∈O(log k) operací se strukturou na prvek vstupu, takže O(n log k) operací celkem, při nichž vznikne O(n log k) kódů. Pomocí kódů tedy můžeme indexovat pole a pamatovat si v něm první výskyt kódu; na inicializaci pole budeme mít dost času.
Pokud jako datovou strukturu zvolíme vyhledávací strom, jedna operace s ním potrvá O(log(n log k)) ⊆ O(log n2) = O(log n). Celý vstup tedy projdeme v čase O(n log n log k). Jestliže místo stromu použijeme hešovací tabulku, projdeme celý vstup v průměrném čase O(n log k).
Persistence
Rovněž stromečkové řešení můžeme upravit, aby mělo složitost O(n log k) i v nejhorším případě. Opět zabere nahradit online dotazy na datovou strukturu přihrádkovým tříděním. Ještě se ale musíme vypořádat s tím, že kódy vrcholů závisí na kódech jejich synů, což vynucuje nějaké pořadí přidělování kódů.
Stromečky zpersistentníme – kdykoliv budeme chtít přepočítat nějakou cestu, nebudeme upravovat existující vrcholy, nýbrž si pořídíme kopii cesty (každý vrchol cesty kromě listu bude ukazovat na jednoho syna v kopii cesty a druhého syna v původním stromu). Takto na každé hladině vznikne celkem O(n+k) = O(n) vrcholů. Pro každý vrchol si zapamatujeme jeho hloubku, identifikátor (v rámci hloubky budeme vrcholy číslovat sekvenčně) a identifikátory synů. Pro každou pozici ve vstupu si zapamatujeme aktuální identifikátor kořene.
Až projdeme celý vstup, začneme kódovat. Budeme postupovat po hladinách od listů ke kořeni, každá hladina bude mít své vlastní kódy. Listy zakódujeme do jejich hodnot. Na každé další hladině vrcholy přepíšeme na dvojice obsahující kódy synů (ty najdeme podle identifikátorů synů), doplněné o identifikátor vrcholu. Dvojice setřídíme lexikograficky, přidělíme jim kódy a zapíšeme je k vrcholům.
Jak dlouho potrvá třídění? Jelikož na nižší hladině je O(n) vrcholů, přidělili jsme jim O(n) kódů; listům přidělujeme kódy jinak, ale také jsou v rozsahu velkém O(n). Třídíme tedy nejvýše O(n) dvojic čísel o velikosti O(n), což zvládneme v čase O(n). Toto opakujeme na O(log k) hladinách.
Celý algoritmus má tedy časovou složitost O(n log k) v nejhorším případě, stejnou jako řešení metodou Rozděl a panuj.